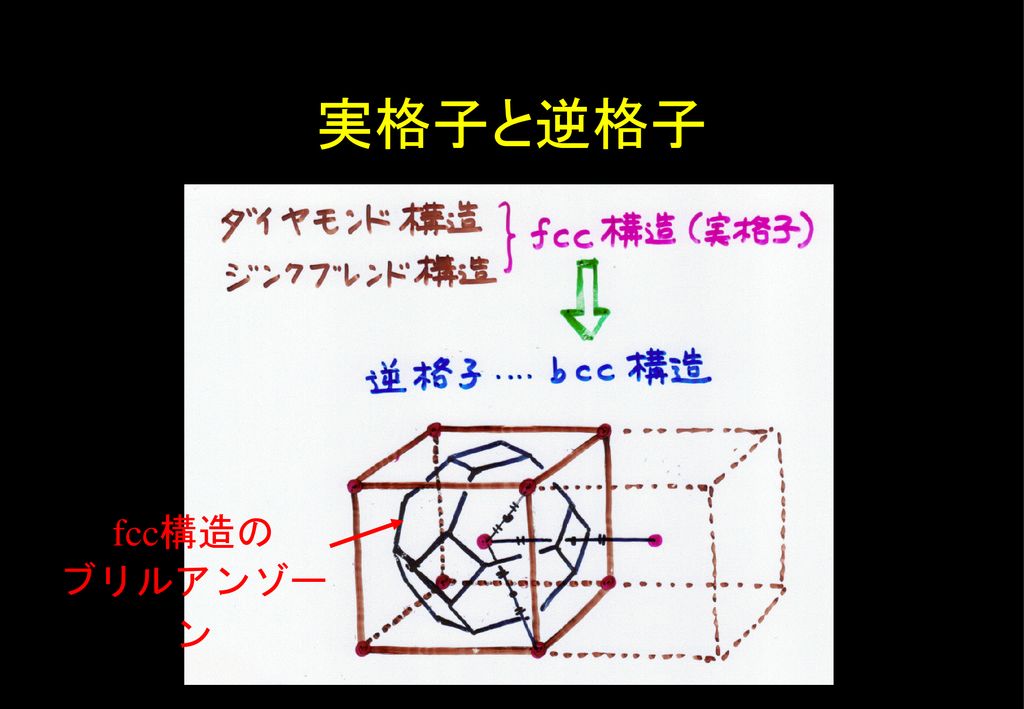
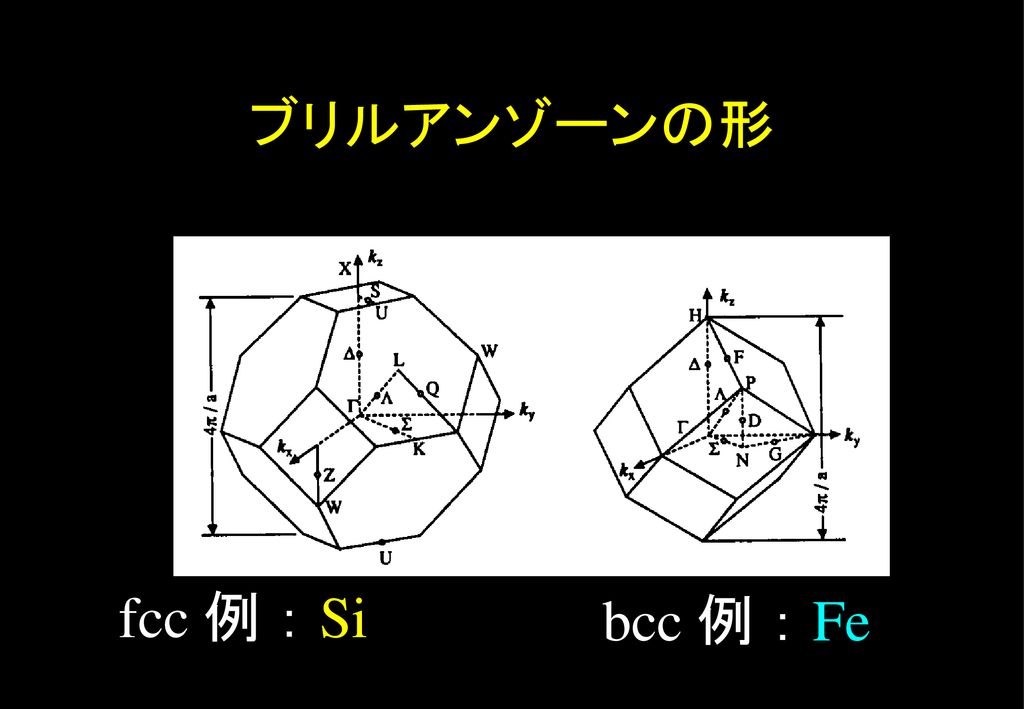
第2講 -エネルギーバンドとブリルアンゾーン- 1 はじめに 前回は一様なポテンシャル中を運動する電子の振る舞 いをポテンシャル0(V(r)=0)の下でシュレーディン ガー波動方程式を解くことによって明らかにした。そ の結果、電子の波動関数は平面波 ( ) exp( )r kr A i で記述され、その第2ブリルアン・ゾーンの配置を変えると、第1ブリルアン・ゾーンと同じ形になる 612 面心立方格子 fcc G L X U X K W G P N H 体心立方格子bcc G A H K M 六方格子 hex X D L S D L S D S L 記号:対称性の高い点 表面上の点:ローマ字 内部の点:ギリシャ文字 いずれも大文字 613 回析実験 未知の逆格子 実格子と逆格子 ブリルアンゾーン境界 ブリルアンゾーンの形 Siのバンドと ブリルアンゾーンの対称点 (3)屏風のようにつながっているのはなぜ? (4)半導体・金属・半金属・ハーフメタル 半導体・半金属・金属・ハーフメタル ハーフメタル:PtMnSb PtMnSbの磁気光学スペクトル (5) Γ25とか
Www38 Tok2 Com
ブリルアンゾーン 意味
ブリルアンゾーン 意味-ブリルアン・ゾーンの境界でエネルギーの縮退がとける 逆格子ベクトル エネルギー・バンド、禁制帯(エネルギー・ギャップ)の形成 第1ブリルアン・ゾーン 102 fcc * L X U X K W X ' / 6 Si のバンド構造 間接遷移型 103 GaAs のバンド構造 直接遷移型 104 0 k E エネルギー バンド 禁制帯 電子のンゾーンの大きさを示す。π/a は、GaAs 結晶お よびAlAs 結晶のブリルアンゾーンの大きさを 示す。 図14 図13 内の(ac)のモードのゾーンセン ター(qz=0)における格子変位パターン。(a) 第 一折返しAlAs 型LO フォノン。(b) 第一折返 しGaAs 型LO フォノン。(c) 下分枝




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬 章 洋介 長岡 本 通販 Amazon
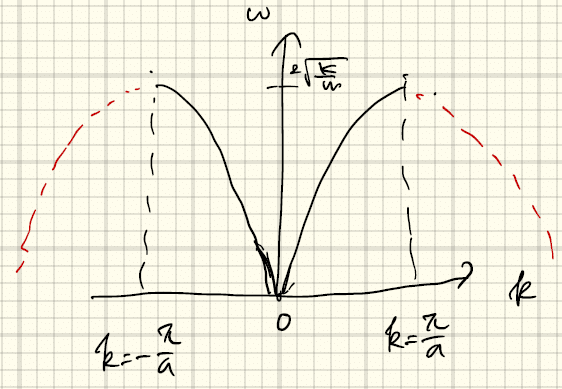
124 ブリルアンゾーンとゾーンフォールディング 4 125 粒子性と群速度 ーが変位の2 乗に比例することを意味する.なお,この系の境界条件として数学的に取り 扱いやすい周期境界条件(ボルン・フォンカルマンの条件)を課す. この系の原子の運動を1 次元的なものに限定すると,運動27.エネルギーギャップの意味 28.3次元結晶の表し方 29.3次元バンド理論 30.逆格子 31.ブリルアンゾーン 32.3次元結晶のエネルギーバンド 33.孤立した原子からの近似 半導体の性質 34.導体と絶縁体 35.伝導電子の数この物理的意味は以下のように考えられます.結晶中のある点の状況は,その点を結晶格子の 整数個分だけずらした点の状況と全く同じです.そのため直観的に,両方の点の周囲において 電子の波動関数は同じ形状となっていおり,物理量は格子定数倍ずれたところでも一致すると 考えるのは
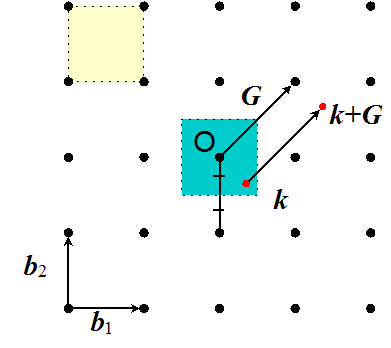
物性物理学序論 筑波大学 自然学類 担当; 舛本 泰章 自然学系棟B609 TA ; TEXT Condensed Matter Physics (凝縮系の物理) Solid State Physics (固体物理学) キッテル 固体物理学入門(丸善),上下ブリルアンゾーン である。 説明するために、まずは簡単に、下の図のような二次元の正方格子を考えよう。 b1,b2 b 1, b 2 は逆格子ベクトルの基底 (逆格子空間の基本並進ベクトル) である。 任意の逆格子ベクトルは G = n1b1 n2b2 G = n 1 b 1 n 2 b 2 と書けるのだ。 ブリルアンさんが思いついたのかどうかは知らないが、原点まわりで図の青い領域だけを考えれば、他の領域はどんな点でも逆格グラフェンにおいては、ブリルアン ゾーン内でギャップの閉じる点(Dirac コーン)が、同等な 点を除いて2カ所あり(K点、K'点)14)、これらは独立な2個 のDirac フェルミオンと考えられる(フェルミオンダブリ ング)。このダブリング注意して奇数のホール伝導
などを参照していただく。ブリルアン・ゾーンを自分で描きたいの であればMathematicaのノートブックMakeBZnbで書ける。 g2 g1 g3 L G W K X U 図1 FCCのブリルアン・ゾーン バンド計算、DOS計算などはプログラムpwbcdで計算する。pwbcdに関する入出力ファイ ルの関係は図4のようになっている。計算の後の 基本並進対称ベクトルから逆格子ベクトルを作ります。 逆格子ベクトルは並進対称ベクトルと双対ですから、どちらも格子の対称性を表しています(互いにフーリエ変換の関係)。 逆格子ベクトルから作る格子の中で最も小さい空間(ウィグナーサイツセル)を作ると、それがブリルアンゾーンになります。 結晶の波動、電子の波動等を考える時に、重要になります。 ナイス! あわせて知りすでに述べたように、 第一ブリルアンゾーンは、逆格子原点のまわりのボロノイ多面体として定義される。 そこで、下中右図のように、 原点と他の逆格子点との垂直二等分面を全て点線で描いてみる。 これらの垂直二等分面が原点の周りで作る最小 の多面体が「第一ブリルアンゾーン」であり、下右図の太い六角形となる。 注:この結果、第一ブリルアンゾーンの六角形状の向きは実格子の格子点



周期境界条件 ボルン フォン カルマン境界条件 波数kとは ばたぱら



半導体物理学
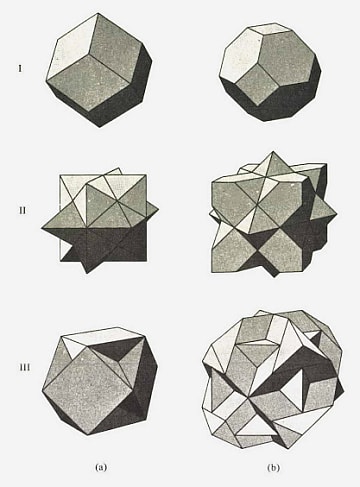
第 n ブリルアン・ゾーン 二次元正方格子 第1BZ 第2BZ 第3BZ fcc格子 (逆空間は bcc) フェルミ面は、 ブラッグ面で切り離される。 27 原点との間に、 ブラッグ面が n−1 枚ある領域 を、 『第 n ブリルアン・ゾーン』 と呼ぶ。 fcc格子のフェルミ面 28 Ne/Nuc= 1 Ne/Nuc= 2 Ne/Nuc= 3 Ne/Nuc= 4 第1BZ 第2BZ 第3BZ 周1 第0章 序 01 諸定数 アボガドロ(Avogadro)定数:NA = (74) 1023mol 1 ボルツマン(Boltzmann)定数:kB = (79) 10 23m2kgs 1K 1(J K 1) 気体定数 R= NAkB = (48)JK 1mol 1 プランク(Planck)定数 h= (81) 10 34m2kg=s(J s);ℏ = h=(2ˇ) 電子の静止質量:me = (11) 10 31kg 電子の素電荷 e= (98) 10 19Cブリュアンゾーンは固体物理学において、波の散乱による回折条件を表現するために広く用いられている。 これは、電子のエネルギーバンド理論などの説明に便利である。 たとえば波数ベクトルがブリュアンゾーン上にあるとき、電子波の ブラッグ反射 が起きる。 結晶内の電子とブリュアンゾーン 量子力学 では、波動関数をψとし、 R を実空間での結晶内の適当な実格子ベクトルとすると、 対称



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



Www38 Tok2 Com
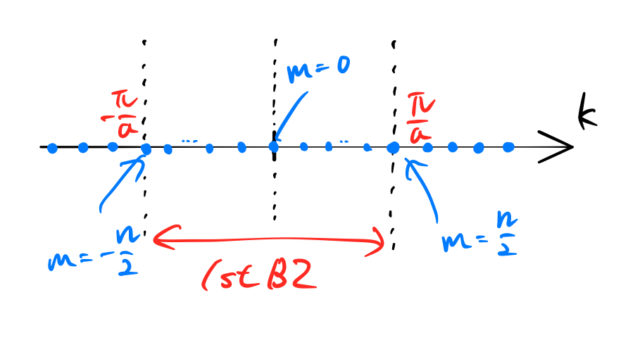
ることを意味する。これを第一ブリルアンゾーンという。 E ika i n ika n a a i k ik a ik a k k e e x x a → = = ⋅ ′⋅ ⋅ π π ψ ψ 2) 2 (() ・・(14) 金属 伝導帯 N L a L a = / (2 / ) (2 / ) π π 個状態数 E 伝導帯 = 個の状態数 半導体 E 価電子帯 E 伝導帯 絶縁体 図3:第一ブリルアンゾーン k a π − a π 図4:周期ブリルアン・ゾーン 固体中の電子にとって、 k = k G で表現されるブラッグ面が、重要な意味をもつこ とがわかった。従って、このブラッグ面に合わせて逆空間の繰り返しの単位胞を設定す ると、何かと都合が良い。無数に存在する逆格子ベクトルG のひとつひとつに、対応す るブラッグ面がブリルアンゾーン あるため、kとkGは等価であり、これは第一ブリユアンゾーンのみを考えればよいことを意味する。 k点 ブリュアンゾーン内においてメッシュによって区分された各点(Sampling points)のことをk点(kpoint)と呼ぶ。ブリュアンゾーン上のk点のうち、対称性の良い点に特に名称




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬 章 洋介 長岡 本 通販 Amazon



固体物理の基礎 上 1 固体電子論概論 アシュクロフト マーミン とね日記
3 ため、自由電子を表すとして、 係 数を( - )にとった。 y,z に 関 しても、同様の 扱 いを後で 行 う。 ( ) 2 ( ) 2 ( ) 1 2 2 2 2 2 2 2 x k x mE x mE x x x x x x x x x x x x φ φ φ φ φ =− =−リルアンゾーン(miniBrillouin zone)の形成である。 A/B超 格子では、A 層の層厚をd A、B 層の層厚をd Bとすると、積 層方向(z方向と定義する)にナノメートルオーダーの人 工的周期(D= d A d B) が生じる。 この超格子周期は、バル ク結晶の格子定数(a 0:04 ~07 nm程度)よりも長いた めに、積層方向のブリルアンゾーンの領域(-π/D ≤k z ≤π/D) は、バルク結晶よりも顕著に小さいものとそのブリルアンゾーンは図2(b)の様によく知ら れるfcc のものとほぼ同じ形を持つ.結晶変位の 無いfcc であればT点はL点と同じ対称性を持つ が,わずかな結晶変位の為,両者は等価でなくな る.L点は1 間隔で3つあるのに対し,T点は 1つだけである.
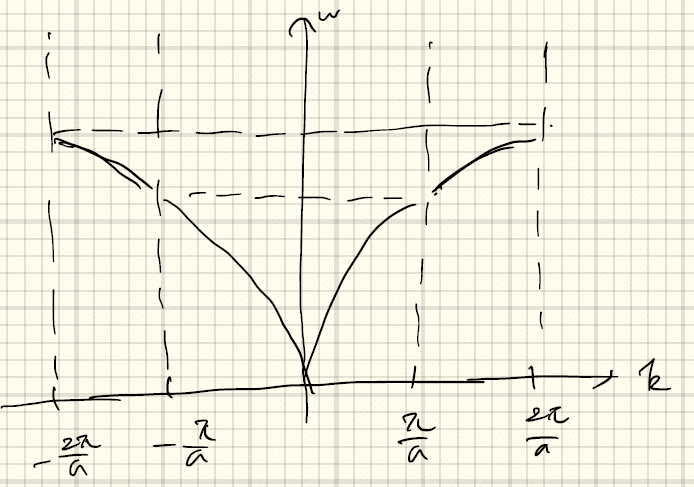



物性物理学1 4 格子振動 フォノン Yukishiomi Note
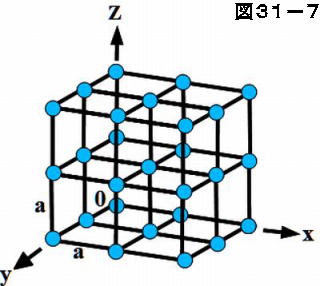



半導体物理学
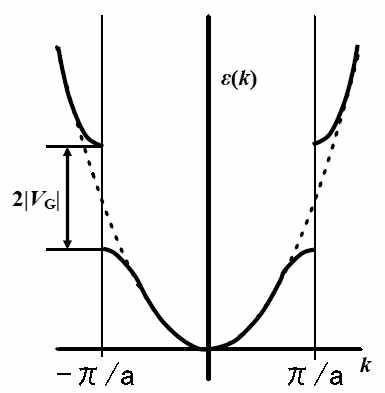
したがって、逆格子ベクトルが異なる波数ベクトルは、同じブロッホ状態のセットを特徴付けるという意味で同等です。 第一ブリルアンゾーンは、 の値の制限集合である K それらのどの2つが同等ではない、まだすべての可能という特性を持つ kは 第一ブリルアンゾーン内の1つ(1つのみ)のエネルギーが高くなり、ブリルアンゾーンの境 界で折り返す。最外殻の電子軌道にはほぼ 同じエネルギーと運動量の電子がつまってい て、そのエネルギーに対応する軌道の半径 によって格子定数が定まる。 シリコン結晶のフェルミ面 結晶には多数の対称面があるため、実際のブ ルリアンゾ�井戸層の場合はV=0)を意味している.図2は,上記のKP ミニブリルアンゾーン端である 点や高次のミニバンドの光学遷移につい ては,光変調反射(photoreflectance PR) 分光法や電場変調反射 (electroreflectance ER)分光法などの変調分光法による測定が極めて有力で ある5, 1 4 ~).変調分




ウィグナー ザイツセルとブリルアンゾーン 化学徒の備忘録 かがろく 化学系ブログ
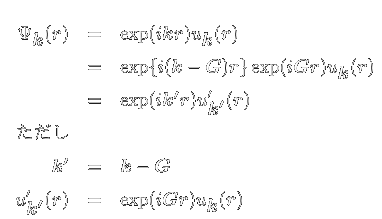



バンド描像
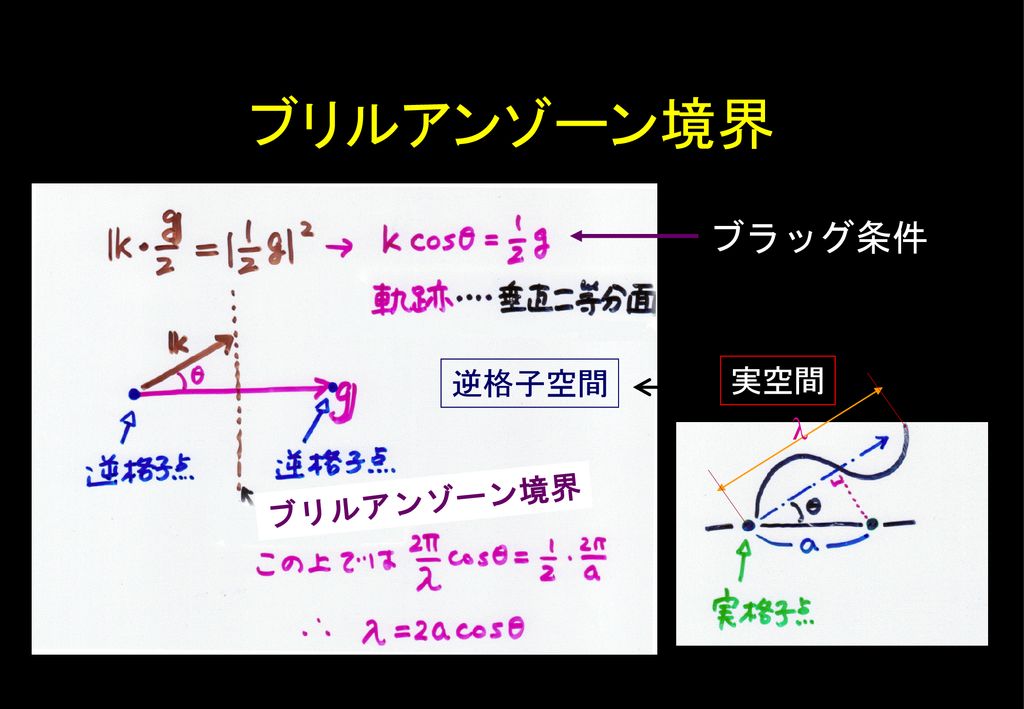
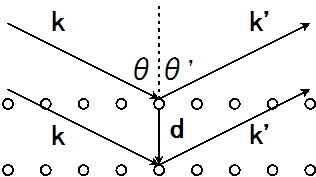
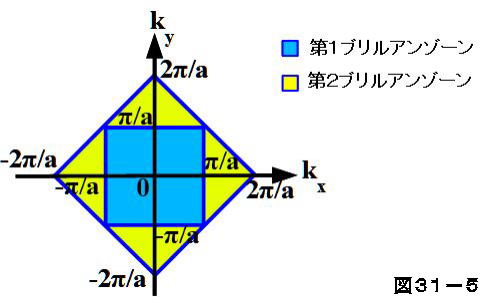
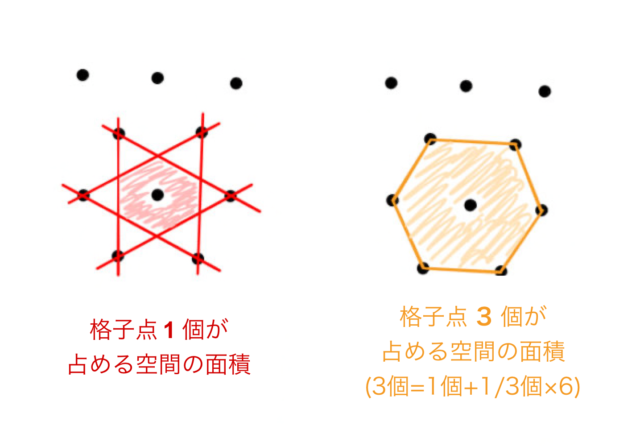
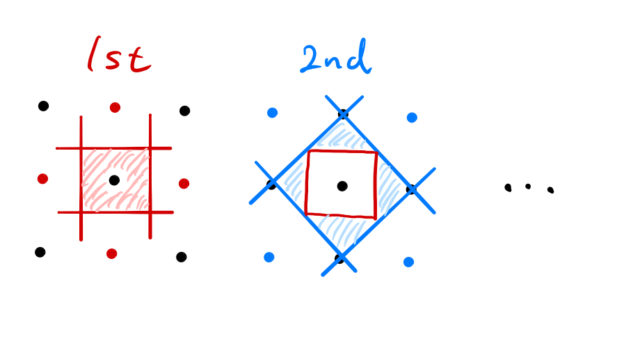
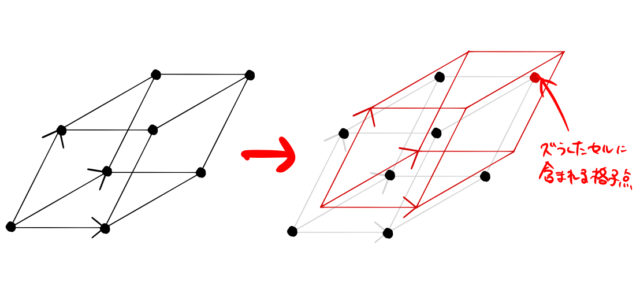
ブリュアン・ゾーンの境界面では、必ず電子のエネルギーは となる。 その外側が第2ブリュアン・ゾーン、第3ブリュアン・ゾーン・・・ 原点を含む領域を第1ブリュアン・ゾーン、 2次元の例 垂直二等分する面で構成される領域をブリュアン・ゾーンと呼ぶ。 逆格子空間において、 の原点と他このとき1stブリルアンゾーンの意味を考える。 ウィグナーザイツセルの取り方から以下の重要なことがわかる。 ポイント 1stブリルアンゾーンを単位として全空間を埋めることができる。 つまり、1stブリルアンゾーンの面積は空間において1個の逆格子点が占める領域の面積と同じである 上の図にあるような赤い六角形はとなりの格子点でも同じ形をしている。 したがって、全空間を1stブリルアンいうことを意味しています。 (11) ここで n は正の整数 は波長 d は格子面の間隔 は視射角(入射角の余角) です。式 (11) はブラッグの式と呼ばれます。 あれ?θ って入射角じゃないの?と思う人もいるかもしれませんが,光学の分野で「入射 角 incident angle」とは,反射面の法線方向と光線




Paypayフリマ ブリルアンゾーンとは




ブリルアン ゾーンとはの通販 柳瀬 章 紙の本 Honto本の通販ストア
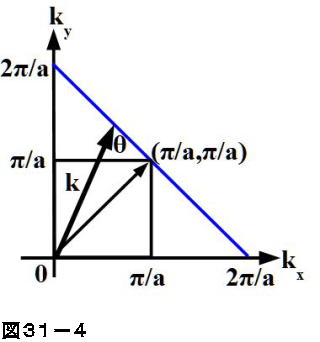
ブリルアンゾーン 逆格子空間のWignerSeitz cellを「ブリルアンゾーン」と呼ぶ。ブリルアンゾーンはWignerSeitz cellと同様の方法で得ることができる。つまり、隣接するすべての逆格子点への線分を引き、それらを垂直二等分する平面で囲まれた多面体が半導体物理学 31.ブリルアンゾーン 1次元の場合、格子の周期が a a であれば、電子波の波数 k k の範囲 −π a < k < π a − π a < k < π a を第1ブリルアンゾーンと呼ぶことは26項で示しました。 それでは3次元の場合はどうなるでしょうか。 その前に2次元で考えてみます。 前項で示したようにブリルアンゾーンの境界ではブラッグ条件 nλ = 2asinθ n λ = 2 a sin θ が成り立ちます。 第1ブリルアンゾーブリルアン帯(ゾーン) (英語表記)Brillouin zone 法則の辞典 「ブリルアン帯(ゾーン)」の解説 ブリルアン帯Brillouin zone 結晶格子中の 波動 の 伝播 における 波数ベクトル 空間内の 逆格子 の基本 領域 のこと.この領域の外の波数ベクトルは,領域内のものと等価である. 出典 朝倉書店法則の辞典について 情報 関連語をあわせて調べる ブリュアン帯 (ゾーン) ブリュアン効果



Sci U Hyogo Ac Jp



フェルミ面とは 物理のかぎしっぽ
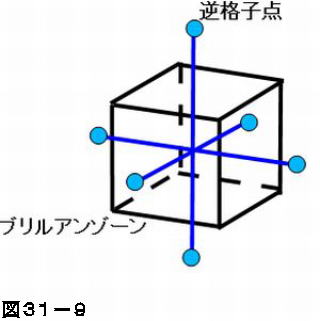
Title 物質科学における群論入門 対称性原理か ら物性予測まで(第61回物性若手夏の学校 講義) Author(s) 岸根, 順一郎 ブリルアンゾーン 逆格子空間におけるウィグナー・ザイツセルをブリルアンゾーン (ブリュアンゾーン、Brillouin zone) という。つまり、逆格子点同士を結ぶ線分を垂直に二等分する面で囲まれた領域がブリルアンゾーンである。特にブリルアンゾーンの中でも最小のブリルアンゾーンを第一 結晶構造,結晶系とブラベー格子,結晶の表現方法,ブリルアンゾーン, 何故逆格子が必要か §2 結晶中の波動 ・・・・・・・・・・・・・・・・ 13 結晶における波動の量子性,音波=フォノンと格子比熱 §3 電子帯の形成 ・・・・・・・・・・・・・・・・ 電子帯とは,補足−原子と



田仲研 Topological Insulator




バンド理論の勉強 武内 筑波大
よって調和近似で考えたフォノンは、素励起としての意味 は第一ブリルアンゾーンに限られる は任意 熱エネルギー密度 () (積分は第一ブリルアンゾーンについて) (積分はすべての について) 光子の熱エネルギーの式は、デバイ近似のフォノンの式と似ているが、以下の点が異なる。 光子で




運動量分解隠れ次数ギャップはuru2si2における対称性の破れとエントロピー損失の起源を明らかにする 自然通信 コミュニケーション 22




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬 章 洋介 長岡 本 通販 Amazon



Www38 Tok2 Com
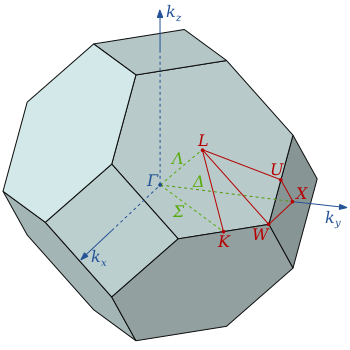



ブリュアンゾーン Wikipedia



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



物理とか 結晶における回折条件




ブリルアンゾーンの意味 用法を知る Astamuse



Maya Phys Kyushu U Ac Jp



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



固体物理の質問です 全然分かりません 本当にお願いします 同種原 Yahoo 知恵袋




ブリルアン Buri Ruan 英語 意味 英語訳 日本語の例文




単斜晶系格子構造のkパスを導出する方法は



Home Hiroshima U Ac Jp



半導体物理学



Ocw Nagoya U Jp



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



正方格子のブリルアンゾーンの端のエネルギーギャップに関する問題 Yahoo 知恵袋



物性物理学1 4 格子振動 フォノン Yukishiomi Note




材料選択範囲の拡大手段 その3 石くれと砂粒の世界



Introduction Of The Electronic Structure Calculation For Experimental Researchers



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



バンド描像
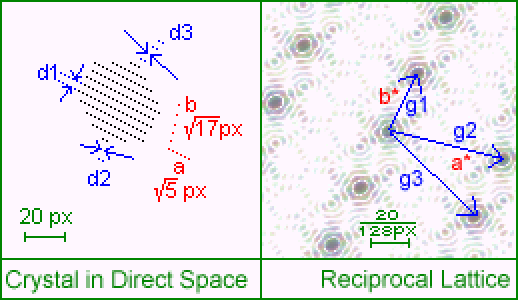



逆格子ベクトル Wikipedia



Www38 Tok2 Com



Important Glossary For Electronic Structure Calculations



en Tohoku Ac Jp



Www38 Tok2 Com



Home Sato Gallery Com




ブリルアンゾーンについて 2次元で第四ブリルアンゾーンがどこを示す 物理学 教えて Goo



フェルミ面とは 物理のかぎしっぽ



金属材料研究所研究部門の研究 東北大学金属材料研究所附属量子エネルギー材料科学国際研究センター




逆格子 逆格子の基本ベクトルの定義と関係 化学徒の備忘録 かがろく 化学系ブログ



Home Hiroshima U Ac Jp
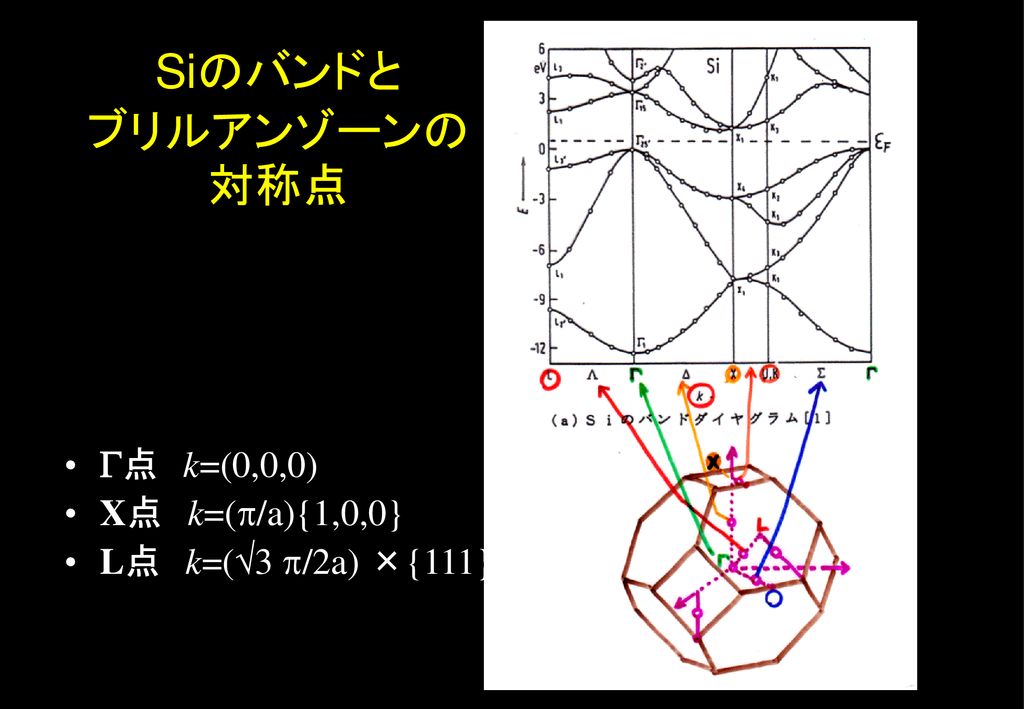



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



Www38 Tok2 Com



Www38 Tok2 Com



Ocw Nagoya U Jp



Xdocs Net




14 号 半導体装置 Astamuse
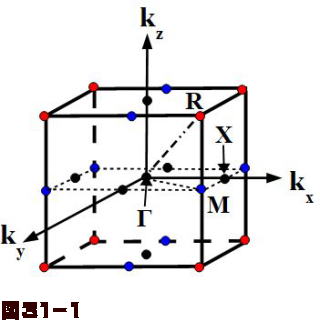



半導体物理学




ブリルアンゾーン境界の意味 用法を知る Astamuse



Home Hiroshima U Ac Jp
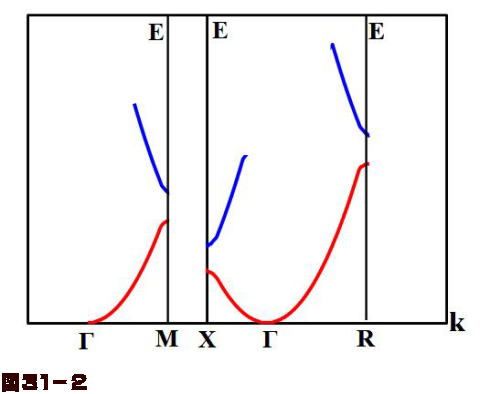



半導体物理学



1




空格子近似 第2 第3及びそれ以上のブリルアンゾーン Weblio辞書




ブリルアンゾーンの意味 用法を知る Astamuse



1



Home Hiroshima U Ac Jp
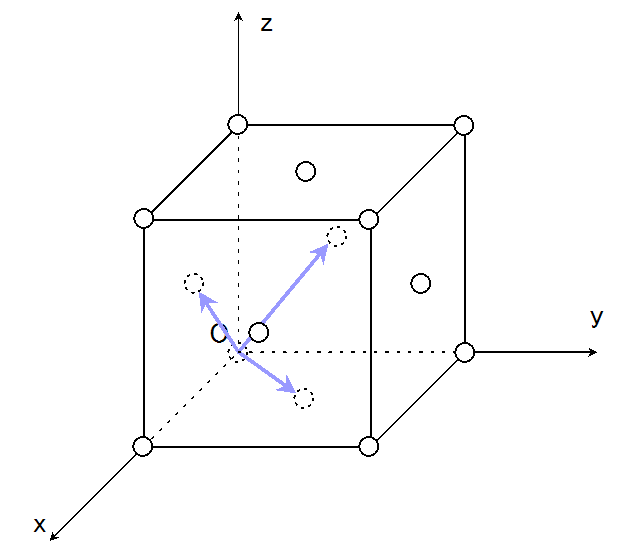



物理とか 逆格子 逆格子ベクトルの例



Home Hiroshima U Ac Jp



Www38 Tok2 Com
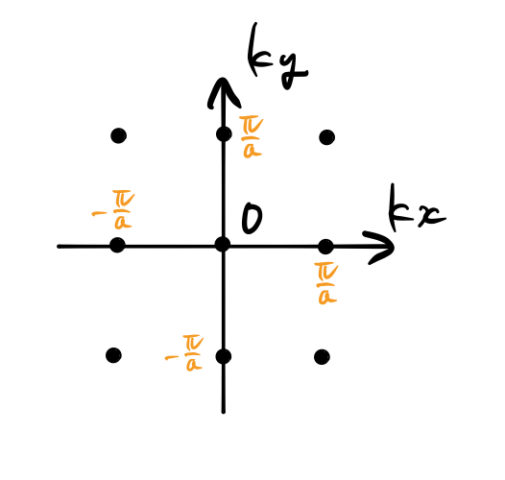



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



Home Sato Gallery Com
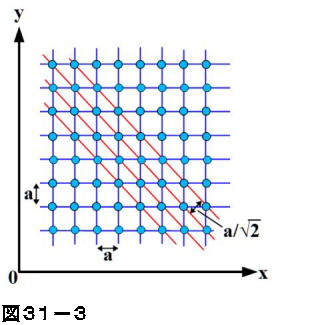



半導体物理学
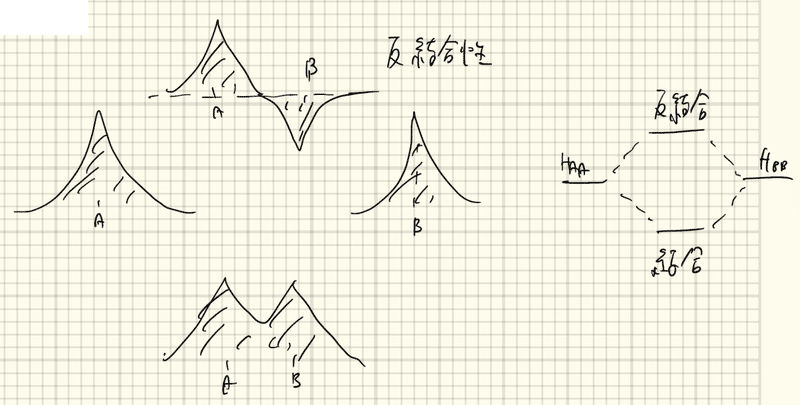



物性物理学1 3 周期ポテンシャル中の 波 としての電子 Yukishiomi Note



Jps Or Jp



Blochの定理に関する補足とブリルアンゾーンの意味 物理とか



Introduction Of The Electronic Structure Calculation For Experimental Researchers




Android 用の 固体物理学 Apk をダウンロード




ブリルアンゾーンの意味 用法を知る Astamuse



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



物性物理学1 2 物質の構造 Yukishiomi Note



半導体物理学
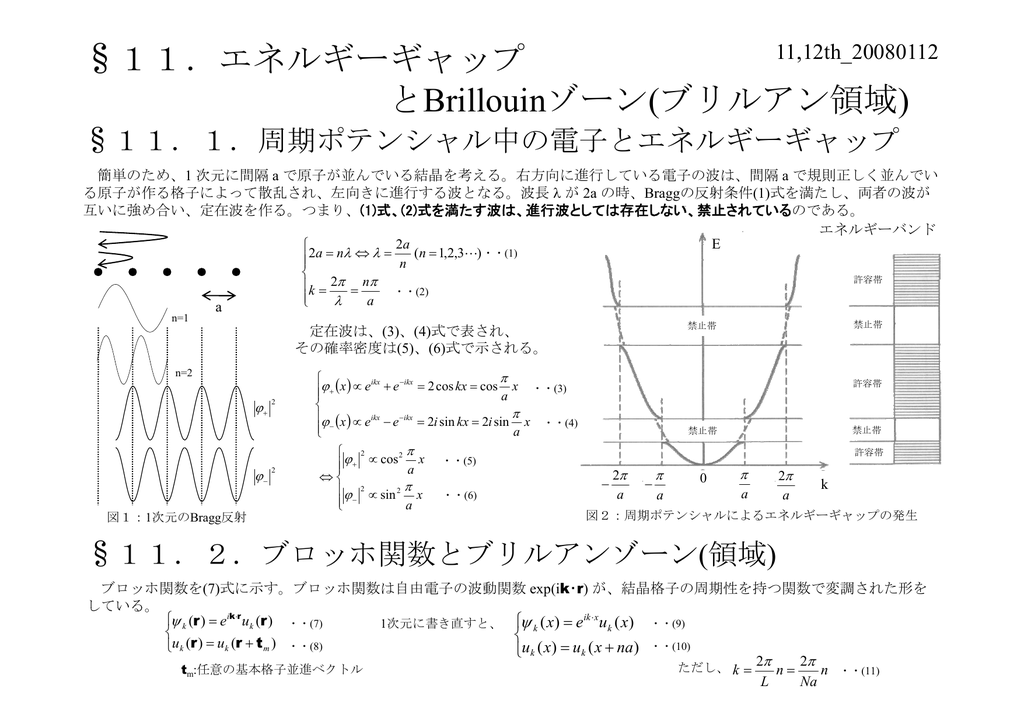



11 エネルギーギャップ とbrillouinゾーン ブリルアン領域 領
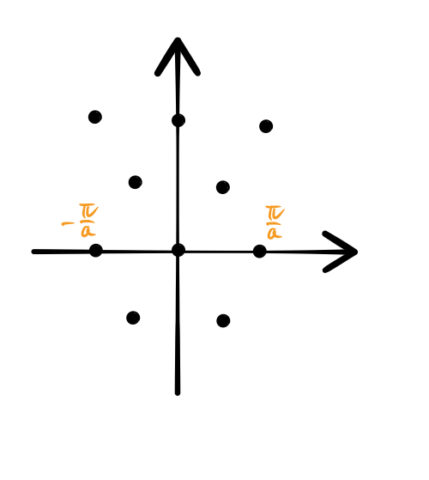



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら
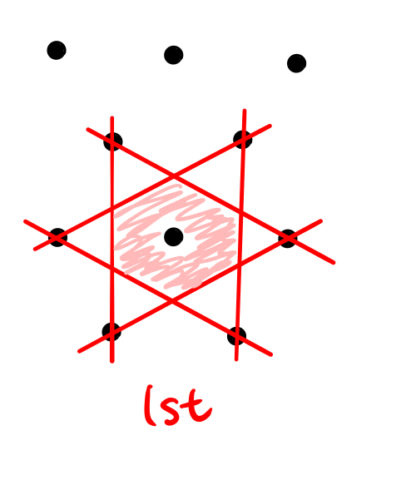



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



Ocw Nagoya U Jp



Www Surface Phys S U Tokyo Ac Jp



ブリルアンゾーンの対称性の高い点 Nano Exit
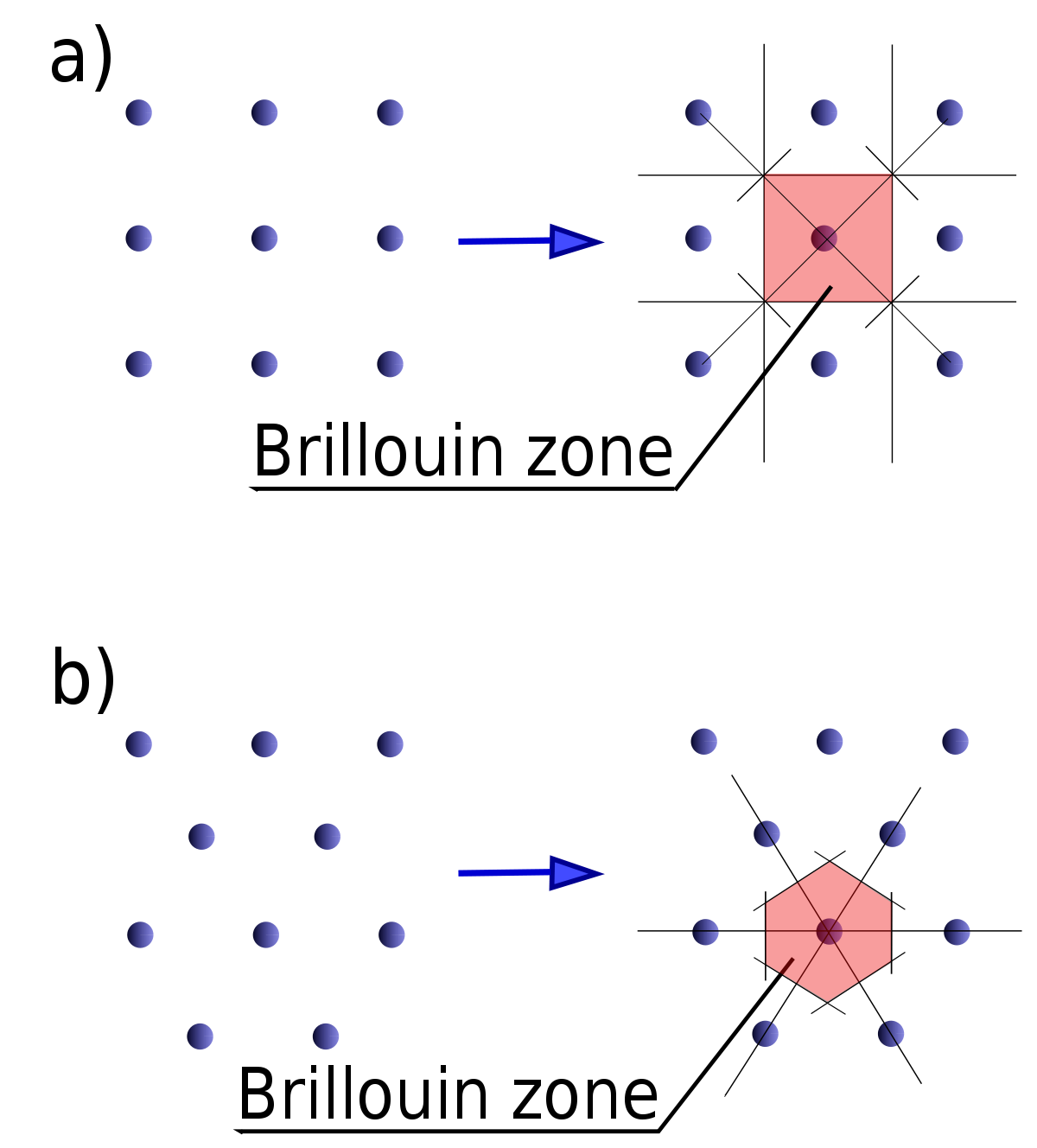



ブリュアンゾーン Wikipedia




空格子近似 第2 第3及びそれ以上のブリルアンゾーン Weblio辞書
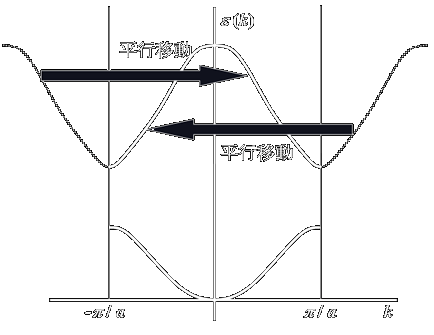



バンド描像



Core Ac Uk




佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



Home Hiroshima U Ac Jp
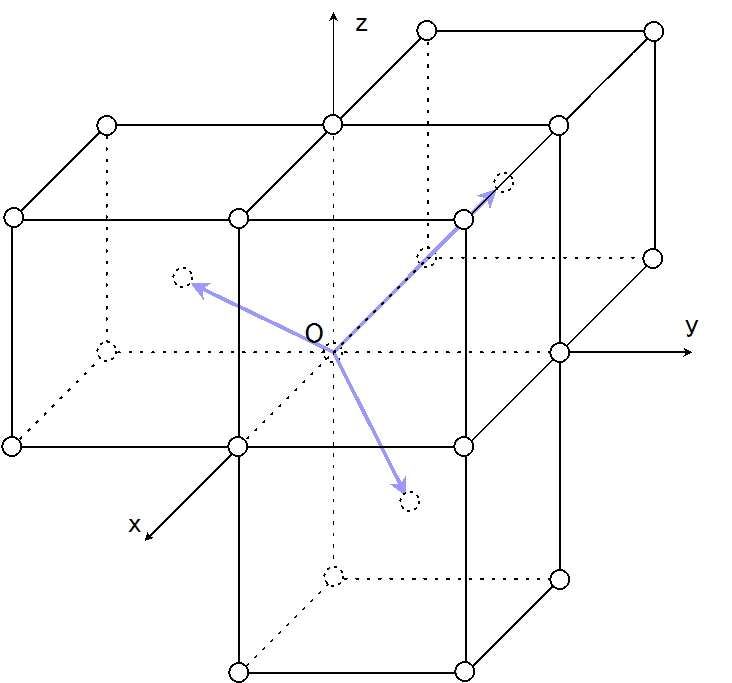



物理とか 逆格子 逆格子ベクトルの例




固体量子41 固体物理連続講義第3回 ブリルアンゾーン Vrアカデミア Youtube




Paypayフリマ ブリルアンゾーンとは



フェルミ面とは 物理のかぎしっぽ



Home Hiroshima U Ac Jp
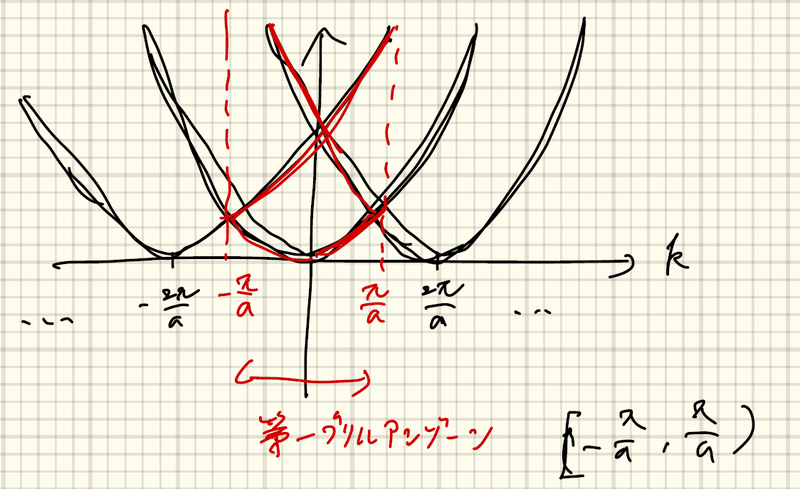



物性物理学1 3 周期ポテンシャル中の 波 としての電子 Yukishiomi Note




ブリルアンゾーンの意味 用法を知る Astamuse




ブリルアン ゾーンとは 柳瀬章 著 本 コミック オンライン書店e Hon




空格子近似 第2 第3及びそれ以上のブリルアンゾーン Weblio辞書




ブリルアンゾーン境界の意味 用法を知る Astamuse



Nims Go Jp



0 件のコメント:
コメントを投稿