[10000ダウンロード済み√] ダイヤモンド構造消滅則 111547

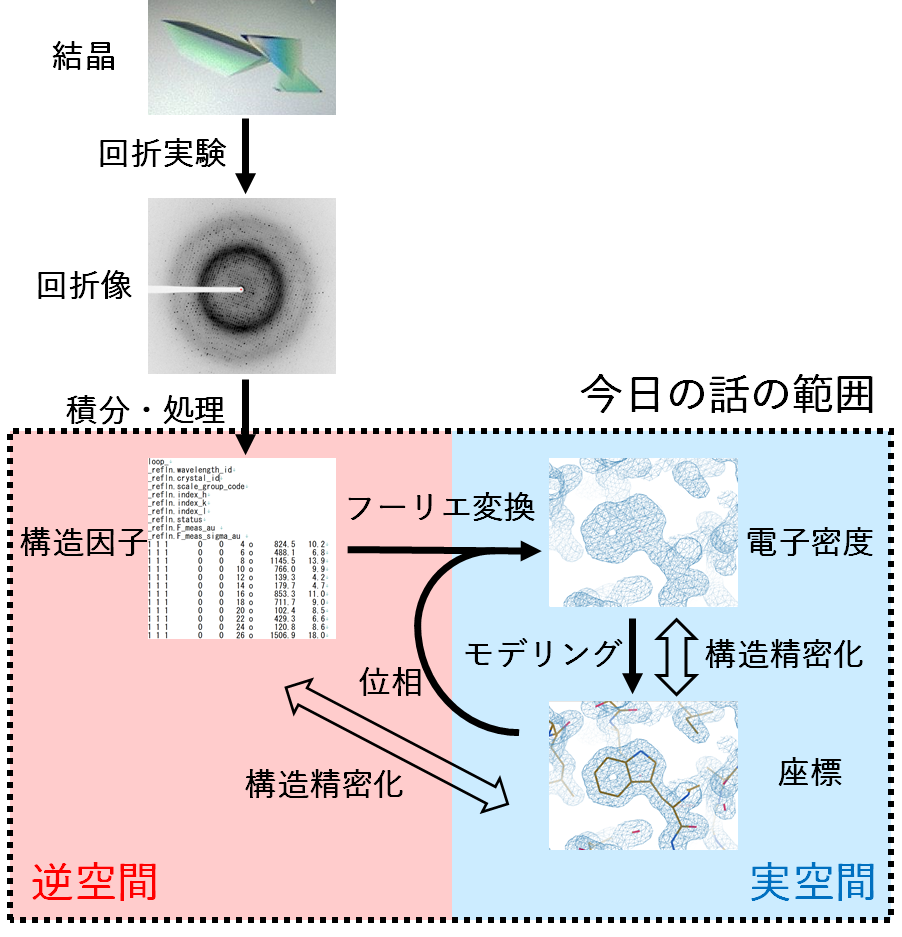
問題16 NaCl の結晶構造（塩化ナトリウム構造という）を調べ、構造因子を計算し選択則を求めよ。Na,Cl の原子形状因子はfNa,fCl とせよ。答塩化ナトリウムは、単純立方格子の各点にNa とCl を交互に並べた構造である。単位格子は、aを格子定数としてNa,Cl をD：ダイアモンドグライド面構造物性研究ではサイトでのReflection Conditionsが全て記載されています。Reflection Conditions（反射条件）は時々消滅則と訳される事があるで、禁制反射（強度が0になる反射）のまとめみたいですが、逆で、禁制反射がある場合空間群と消滅則の対応表備忘録に真面目なメモをします。 X線で結晶構造解析をするときに、消滅則の表がほしいときがある。生きていれば一度や二度はあるよね。私は中性子線でブロックコポリマーのモルフォロジーの解析がしたくて、その表が

61 結晶構造因子ダイヤモンド構造 Youtube

ダイヤモンド構造消滅則

ダイヤモンド構造消滅則- 「X線回折が起きる、起きないを結晶構造因子から考察します。また、その時の指数をミラー指数により求めます。ダイヤモンド構造、ナトリウム型構造の消滅則も載せておきます。」, キーワード x線回折,回折ピーク,結晶構造因子,消滅則,ミラー指数,マテリアル,金属,材料,大学,工学,ブ半導体物理：結晶構造について（2） Posted on 17年5月11日 17年12月17日 by sciencompass34 皆さんこんにちは！半導体物理の紹介をしていきます。前回、結晶構造の基本としてブラベー格子を紹介しました。今回は、半導体として広く使われているシリコン

ｘ線結晶解析におけるラウエの条件式とブラッグの条件式

消滅則を理解するために回折という現象と構造因子という概念が必要だが，この学会誌の読者の中では既知と考えここでは省略する．なお，復習の必要な読者は本誌特集号「x線構造解析を始めよう」，あるいは「単結晶回結晶構造原子の種類結晶子の配向構造解析手掛かり結晶構造イオン半径情報回折線の消滅則格子の型結晶子サイズの測定残留応力測定（セラミックスや金属試料）結晶性格子不整格子欠陥ピーク形状定量分析（結晶混合物、鉱物試料）原子座標ダイヤモンドは面心立方格子の消滅則（hklが全て奇数または偶数のみ観測される）に加え hkl=4m2 のときは消滅というルールが加わるダイヤモンドのバンド構造 26 W Saslow, et al, Phys Rev Lett, 16, 354, (1966)

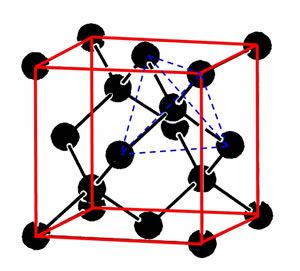
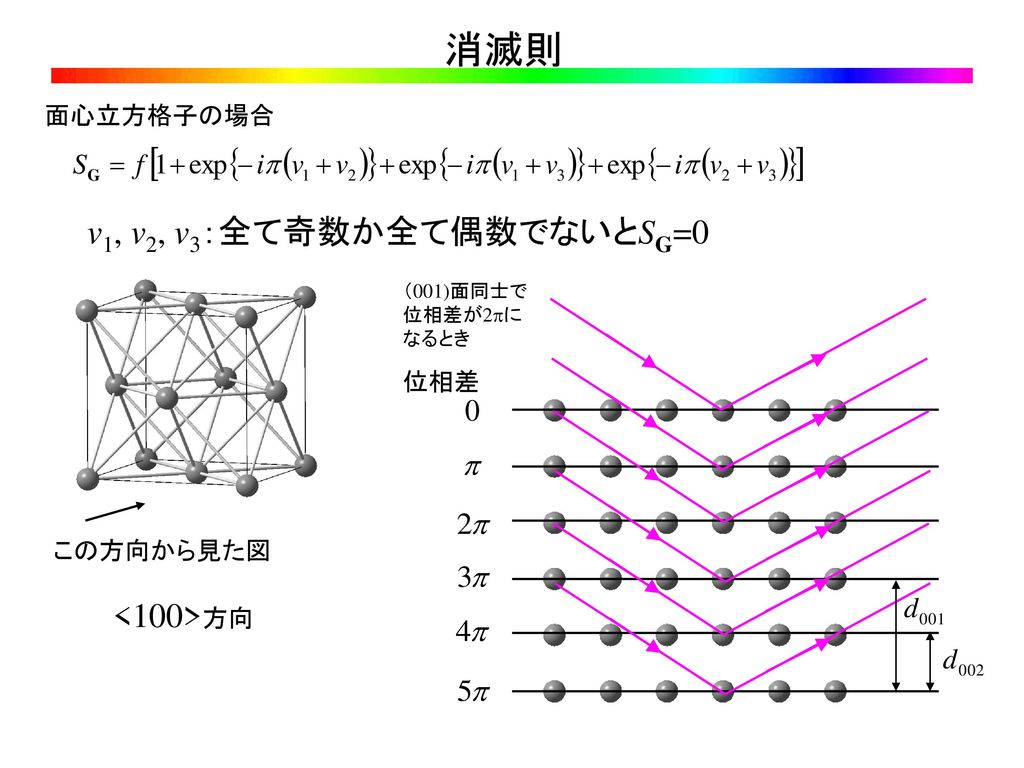
(h00)反射では、 hが2の倍数でないと結晶構造因子が0となる。同様に、 y軸に平行な2 1 らせん軸があれば(0k0)反射に、 z軸に平行な2 1 らせん軸があれば(00l)反射に、それぞれ消滅則が出現する映進操作に由来する消滅則結晶構造解析の筋道＊単結晶に単色X線を当て、回折データ F 収集＊回折データ F に位相を与える＊逆結晶 F ＊フーリエ変換して結晶の構造を求める F ＊逆格子点は周期的に並んでいるが、 F(h,k,l) は周期的でない。＊格子点のみ値 F(h,k,l) 有り。ダイヤモンド型構造ダイヤモンドがたこうぞう diamond structure 立方晶系に属する結晶構造の1種。単位胞の中に8個の原子があり，そのうちの4個ずつが2つの面心立方格子をつくり，それらは互いに立方対角線に沿ってその長さの 1/4 だけ移動した位置を占める。 1つの原子には4個の最近接原子が正

表面構造を回復するためには,酸化あるいは水素化などの化学的処理によって乱れた炭素を除去すると同時に規則的な吸着表面を形成するという手法がとられる。 22酸化表面(酸素を化学吸着した表面) 酸素ガス,酸による湿式酸化によるダイヤモンド表面Diamond 図34 固体の定積比熱*2の温度変化C v(T)。鉛3,4、銅5、ダイアモンド6,7 の実験値。エネルギー等分配則の破れしかし、デュロン＝プティ則を基準に図32 の実験値を見直してみると、軽元素領域で、比熱の異常に小さい物質が目立つ。消滅測を考えるときは、この結晶構造因子が0 のとき $$ F(hkl) = 0 $$ の面指数$hkl$がどうなればよいかを考えます。体心立方格子の消滅測では体心立方格子の消滅測を導いてみましょう。まず、体心立方格子の原子がどこに配置しているかを確認します

Mtl Kyoto U Ac Jp

62 結晶構造因子閃亜鉛鉱型構造 Youtube

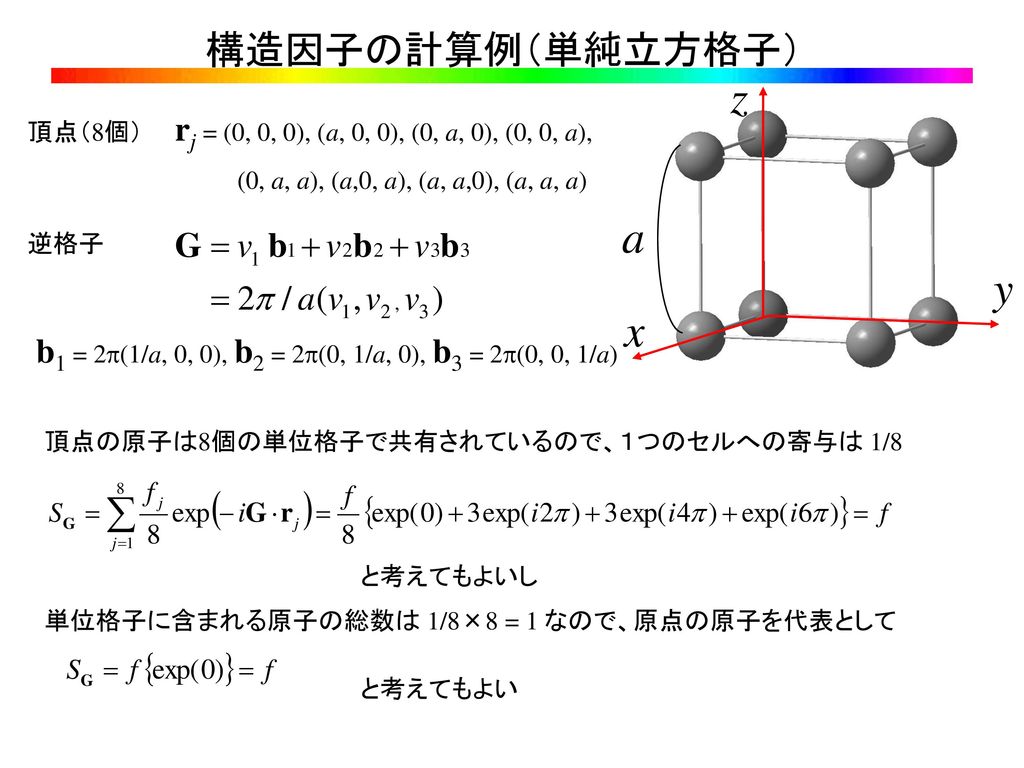
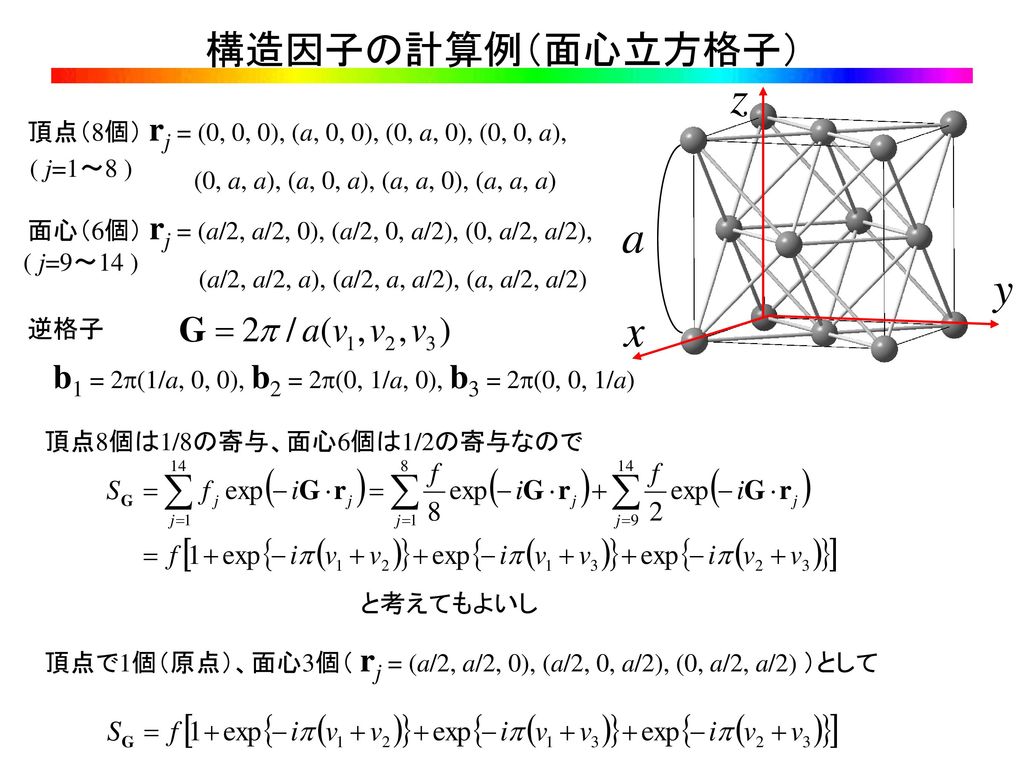
1) ダイヤモンド型構造ダイヤモンド型構造の立方体単位格子は8個の原子を持つ。その空間格子は(0 0 0)の位置を原点とする面心立方格子と(1/ 4 1/ 4 / 4)の位置を原点とする面心立方格子を組み合せて構成できる。 2) 閃亜鉛鉱型構造ダイヤモンド型構造を構成直接格子の構造を理解することができる。 Si単結晶の電子線回折像・ラウエの条件逆格子を用いた回折の条件を求めてみる。ブラッグの条件については既知であると思うが、ブラッグの条件（と等価ではあるが）よりも汎用性ダイヤモンド構造因子消滅則＊格子点のみ値 F(h,k,l) 有り。現れているピークの数と構造因子、(ii)同じミラー指数を持つピークの2θ角の大小とブラッグの条件 2d・sin θ = nλの関係の二つの観点から根拠を述べたうえで、正しい組み合わせを答えなさい。

ダイヤモンドの結晶と欠陥中央宝石研究所 Cgl

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

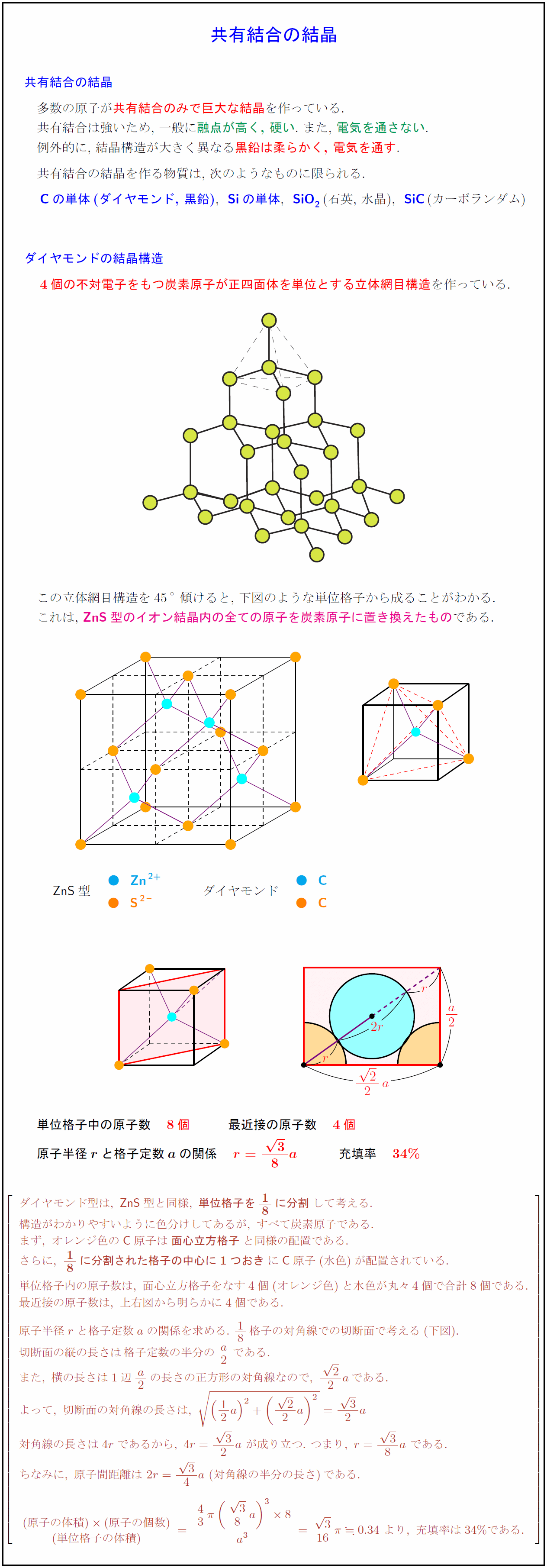
共有結合の結晶（ダイヤモンドの結晶構造）多数の原子が共有結合のみで巨大な結晶を作っている共有結合は強いため,\ 一般に融点が高く,\ 硬い\ また,\ 電気を通さない例外的に,\ 結晶構造が大きく異なる黒鉛は柔らかく,\ 電気を通す共有結合の結晶(2) ダイヤモンド構造のx線回析における結晶構造因子を求めよ。 (3) ダイヤモンド構造において、構造因子が0とならない逆格子点を求め、3次元の点として図示せよ。 (4) 図3のように、ダイヤモンド構造をとる結晶の(111)面にx線を照射した。スクリーン上に回11 結晶構造現実の結晶は最小の繰り返し単位である基本単位格子（primitice cell) で作られている。結晶結晶構造＝空間格子(space lattice) ＋単位構造(basis) 格子＝結晶の周期性により空間に広

Ir Lib Shimane U Ac Jp

Flex Phys Tohoku Ac Jp

6 結晶の表現方法 (1)方向基本格子ベクトルをa, b, c とし，n1, n2, n3 を任意の公約数を持たない整数とすると，ベクトル T = n1 a n2 b n3 c (11) の整数倍によって1つの単位胞を任意の単位胞の位置に移動させて重ね合わせることができる．n1, n2, n3 をダイヤモンド構造 "8 せん亜鉛鉱型構造図 * ウルツ鉱型構造図 *" b 型構造 "8 型構造図 * ペロプスカイト型の結晶図 * a 構造の複雑な結晶 " 6 "8 図 /*72章．固体の結晶構造と構造因子例4 ダイヤモンド，NaCl, CsCl, ．．． F(g)がゼロになる：逆格子点はない（消える） ↓ 消滅則（extinction rule） 24

高校理論化学共有結合の結晶ダイヤモンドの結晶構造受験の月

Information

そこで、ダイヤモンド構造の試料としてSi の粉末、NaCl 構造の試料として食塩、体心立方格子の構造を持つ試料として鉄粉を用意し、その内、Si について測定を行い、ミラー指数、格子定数、面間隔を求めると共に、消滅則の理論用いて結晶構造を決定する。Question 結晶構造の空間群になぜ時間反転を導入する必要があるのかよく分かりません．また，磁気モーメントの対称操作による変換をもう少し詳しく説明して下さい． Answer 図42を環電流として視覚的になるように書き直しました。さ図1ダイヤモンドの結晶構造表1ダイヤモンドの特性密度 3515g/cm3 熱伝導率 00∼2300W/m・K 熱膨張率（25∼0℃） 08∼12×10−6/K バンドギャップ 545eV 電気抵抗率＞1014`cm ヤング率 1050GPa ビッカース硬さ 7600∼ 摩擦係数（空気中） 005∼015 屈折率（波長10mm

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

閃亜鉛鉱構造の構造因子とそれに基づく消滅則を教えてください閃亜鉛 Yahoo 知恵袋

閃亜鉛鉱構造の構造因子とそれに基づく消滅則を教えてください閃亜鉛 Yahoo 知恵袋

未知の構造の決定や構造パラメータの正確な測定回析過程が固体の原子構造の周期的性質に最も敏感線源試料検出器線源： X線電子線中性子線原子線線源と試料の間の相互作用弾性的 elastic エネルダイヤモンド構造グラファイト構造 NaCl型構造 CsCl型構造閃亜鉛鉱（ZnS）型構造 Facecentered cubic (fcc) Bodycentered cubic (bcc)packed Diamond Graphite Zinc blende4 x線回折 1 目的銅の粉末試料を用いたx 線回折測定を行い、粉末x 線回折の測定方法と測定原理について学ぶ。また、得られたx 線回折のデータから格子定数の計算や結晶構造の同定を行えるようになる。あわせて、結晶を取り扱う上で重要な逆格子やミラー指数の概念についても理解する。

高分解能

ダイヤモンド構造の構造因子、また消滅則により残る回折線のミラー指数の求め方を教えてください。回回折線は(001)から(333)までです。解決済み質問日時： 17/5/31 1500 回答数： 1 閲覧数： 2,102 教養と学問、サイエンス > サイエンス > 物理学ダイアモンド格子はこの座標に (1/4,1/4,1/4)を加えた位置に同種原子を置くことで構成されます．そこで (1/4,1/4,1/4)をベクトルdと書くことにすると，追加した原子の位置ベクトルはdri (i=14)．したがって，逆格子ベクトルをGとして構造因子は S = f Σ i=14 { e密構造を副格子として重ねて，一方を (0, 0, 3 c /8) だけずらして重ねた構造がウルツ鉱構造である．この場合も一つの原子を中心としてほぼ正四面体の頂点位置に別種の原子が存在することが分かる．図 1 ･ 1 ダイヤモンド構造 3) 図 1 ･ 2 3)閃亜鉛

ダイヤモンドの結晶と欠陥中央宝石研究所 Cgl

Ir Library Osaka U Ac Jp

繰り返しの単位構造をf0(r) とおき、これを(58) 式のすべての格子点に配置して、電荷分布f(r) を構成する。 f(r) = ∑ R f0(r R) def= ∑ n1 ∑ n2 ∑ n3 f0(r n1a1n2a2n3a3) これを、(57) 式の散乱振幅に代入して、フーリエ変換する。 F(q) = ∑ R ∫ dr eiqr f 0(rR) 積分変数をr 「結晶構造について六方最密構造 NaCl型構造ダイヤモンド型構造閃亜鉛鉱型セシウム型など」, キーワード結晶構造,マテリアル,材料,金属,六方最密構造,ダイヤモンド構造,nacl型構造,面心立方格子,体心立方,セシウム型構造,閃亜鉛鉱,フッ化カルシウム最後の式変形では、デルタ関数の伸縮則(a2) を用いた。周期関数現実的なポテンシャルや電子の存在確率分布には幅があって、デルタ関数にはならない。しかし、(64) 式を積分核として用いると、様々な周期関数とそのフーリエ変換が導出される。

物性なんでもｑａ 1 299

Oit Ac Jp

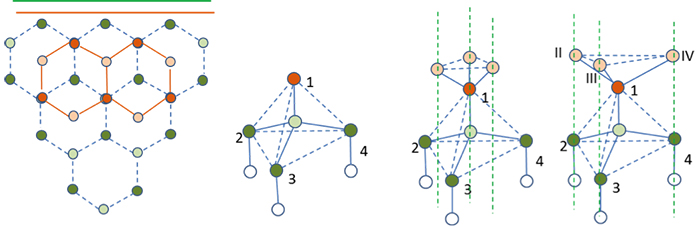
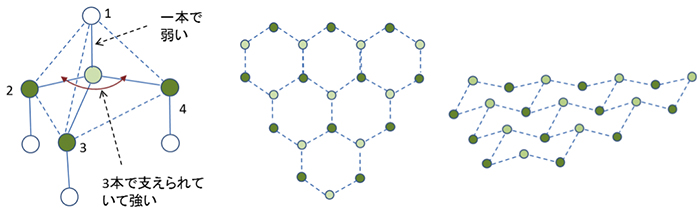
六方最密構造（hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造最密充填構造配位数＝12 最密充填構造配位数＝12 配位数＝8 配位数＝4 sp3 混成軌道の4ボンドの制約下で最密充填最近接原子距離 = 第2最近接原子距離 = a空間群判定の例ー単斜晶系単斜晶系底心格子とc映進面：Cc, C2/c 消滅則なし：P2, Pm, P2/m 2回らせん軸のみ： P2 1, P2 1 /m c映進面のみ：Pc, P2/c 2回らせん軸とc映進面：P2 1 /c 底心格子のみ：C2, Cm 青：ほとんど表れない

Eedept Kobe U Ac Jp

Ir Lib U Ryukyu Ac Jp

ダイヤモンドの結晶構造はちょいとややこしい高校化学の教材分子と結晶模型のベンゼン屋楽天ブログ

ダイヤモンドの結晶構造はちょいとややこしい高校化学の教材分子と結晶模型のベンゼン屋楽天ブログ

ｘ線結晶解析におけるラウエの条件式とブラッグの条件式

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

ダイヤモンド構造の構造因子また消滅則により残る回折線のミラー指数の求め方を Yahoo 知恵袋

ダイヤモンド構造の構造因子また消滅則により残る回折線のミラー指数の求め方を Yahoo 知恵袋

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

Corporate Murata Com

Flex Phys Tohoku Ac Jp

Mdr Nims Go Jp

Home Hiroshima U Ac Jp

Akitsu Ee Ehime U Ac Jp

61 結晶構造因子ダイヤモンド構造 Youtube

Ir Soken Ac Jp

受験理系特化プログラム Xyz

Coral T U Tokyo Ac Jp

受験理系特化プログラム Xyz

Information

ダイヤモンド構造構造因子

Space Group For Crystal Structure Analysis

Space Group For Crystal Structure Analysis

週刊ダイヤモンド 48 Off ダイヤモンド社雑誌電子書籍定期購読の予約はfujisan

週刊ダイヤモンド 48 Off ダイヤモンド社雑誌電子書籍定期購読の予約はfujisan

ダイヤモンド構造構造因子

Ocw Kyoto U Ac Jp

Fccの消滅則の求め方を教えてください面指数 Hkl の結 Yahoo 知恵袋

週刊ダイヤモンド 21年7月17日号週刊ダイヤモンドダイヤモンド社無料試し読みなら漫画マンガ電子書籍のコミックシーモア

週刊ダイヤモンド 21年7月17日号週刊ダイヤモンドダイヤモンド社無料試し読みなら漫画マンガ電子書籍のコミックシーモア

構造因子に関するq A Yahoo 知恵袋

消滅則について解説化学徒の備忘録

ダイヤモンド社新品未開封週刊ダイヤモンド年12 5 決算書100本ノック21の通販 By Aki S Shop ダイヤモンドシャならラクマ

ダイヤモンド社新品未開封週刊ダイヤモンド年12 5 決算書100本ノック21の通販 By Aki S Shop ダイヤモンドシャならラクマ

Space Group For Crystal Structure Analysis

ダイヤモンド構造の構造因子また消滅則により残る回折線のミラー指数の求め方を Yahoo 知恵袋

Home Hiroshima U Ac Jp

Nda Ac Jp

高校化学結晶格子共有結晶ダイヤモンド型理論化学 Youtube

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

Jim Or Jp

Ir Lib Shimane U Ac Jp

Coral T U Tokyo Ac Jp

Information

Home Hiroshima U Ac Jp

前回の内容結晶工学特論第4回目格子欠陥ミラー指数 3次元成長積層欠陥転位刃状転位らせん転位バーガーズベクトル Ppt Download

前回の内容結晶工学特論第4回目格子欠陥ミラー指数 3次元成長積層欠陥転位刃状転位らせん転位バーガーズベクトル Ppt Download

Www3 Muroran It Ac Jp

ダイヤモンド構造の構造因子また消滅則により残る回折線のミラー指数の求め方を Yahoo 知恵袋

Natsci Kyokyo U Ac Jp

Kawasaki Web Nitech Ac Jp

Ir Library Osaka U Ac Jp

Rokakuho Co Jp

Iaea Org

Jst Go Jp

Aeovfrsdcv2mhm

Space Group For Crystal Structure Analysis

ダイヤモンドの結晶と欠陥中央宝石研究所 Cgl

Ir Lib Shimane U Ac Jp

前回の内容結晶工学特論第4回目格子欠陥ミラー指数 3次元成長積層欠陥転位刃状転位らせん転位バーガーズベクトル Ppt Download

Mukiken Eng Niigata U Ac Jp

暗記不要ダイヤモンドの密度の求め方をまとめてみた化学受験テクニック塾

高分解能

ダイヤモンドの結晶構造はちょいとややこしい高校化学の教材分子と結晶模型のベンゼン屋楽天ブログ

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

ダイヤモンド構造の構造因子また消滅則により残る回折線のミラー指数の求め方を Yahoo 知恵袋

Coral T U Tokyo Ac Jp

Information

Nda Ac Jp

Information

前回の内容結晶工学特論第4回目格子欠陥ミラー指数 3次元成長積層欠陥転位刃状転位らせん転位バーガーズベクトル Ppt Download

Natsci Kyokyo U Ac Jp

Mukiken Eng Niigata U Ac Jp

専門講義 X線回折とピーク大学生専門学校生社会人工学のノート Clearnote

Home Hiroshima U Ac Jp

Coral T U Tokyo Ac Jp

Jim Or Jp

Kawasaki Web Nitech Ac Jp

Information

$Solved Substitute Eight Atoms Positions In The Unit Cell Into Intensity Of Diffraction F Hkl Crystal Is Composed Of Same Kind Of Atoms Diamond Course Hero$

Solved Substitute Eight Atoms Positions In The Unit Cell Into Intensity Of Diffraction F Hkl Crystal Is Composed Of Same Kind Of Atoms Diamond Course Hero